けものフレンズBBS NEO

けものフレンズBBS NEO

けもがたり '24 【3・4月号】～日曜動物学者のつどい～ / 330

543 コメント
views
89 フォロー
330
小鉢涼平 2024/04/07 (日) 22:30:35 fe4f3@ef234 >> 304

調べてみましたがなんだか難しい話に行き当たりました・・・
本当は円で作った方が一区画当たりの外周は小さくなるものの無駄な隙間が空いてしまうので
一番近い正六角形にせざるを得ないといった所ですかね？

ハニカム構造
ハニカム構造（ハニカムこうぞう、英語：honeycomb structure）とは、正六角形または正六角柱を隙間なく並べた構造である。ハニカムとは英語で「ミツバチの櫛（＝蜂の巣）」という意味であり、多くの蜂の巣がこのような形をしていることから名付けられた。 広義には、正六角柱に限らず立体図形を隙間なく並べたもの（3次元空間充填）をハニカムと呼ぶ。 板状の素材に孔を開ければ、強度をあまり損なわずに必要な材料を減らすことができる。孔の大きさや数をどんどん増やせば、最終的には棒材による構造が残る。同様に、塊状の素材に孔を開ければ、板材による構造が残る。これらがハニカムである。 ハニカムの形 孔を小さくすれば強度は増すが、単位面積あたり棒材の量は増える。そこで、孔の面積を一定にして、最も棒材の量が少なくなる孔の開け方を考える。これは、 という数学的問題にできる。またこうすることで、強度と材料の量の関係に限らないさまざまな課題に一般化できる。 同じ面積で最も周が短い図形は円である。しかし円で平面を充填しようとすると歪な形の隙間が残り、円だけで充填することはできない。平面充填可能な図形には、三角形、四角形、平行六角形などがあるが、最も周が短いのは正六角形である。これは、平面充填形の中で正六角形が最も円に近いことからも直感的に理解できる。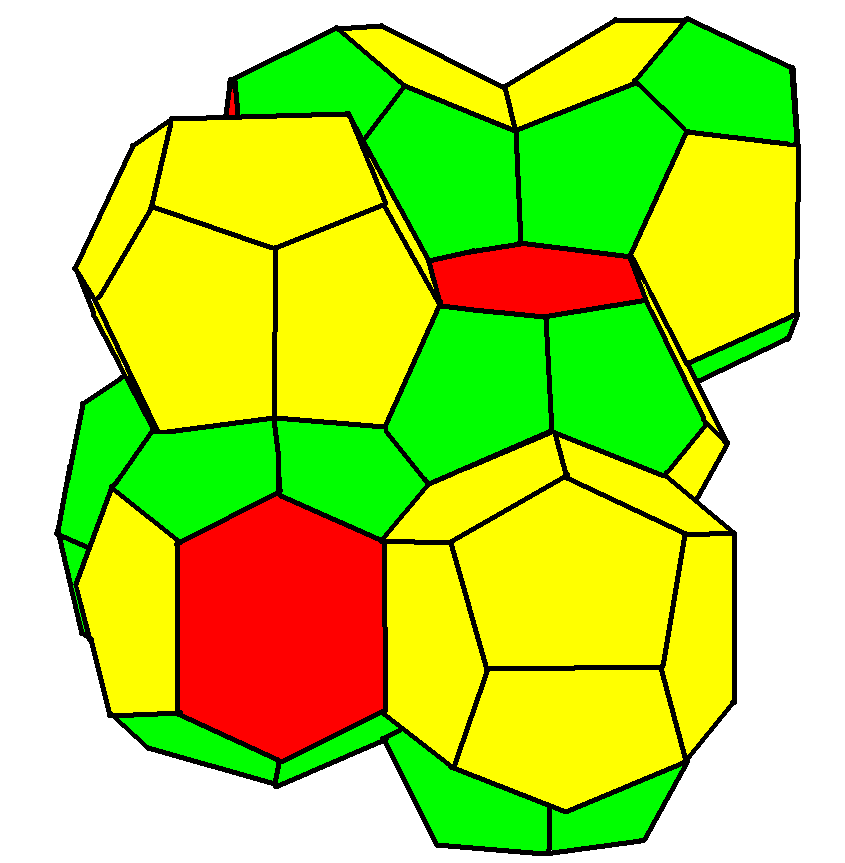 同様に、3次元での という問題（「ケルヴィン問題」）を考えることができる。この問題は未解決だが、既知の最適な答えはウィア＝フェラン構造と呼ばれる等体積の12面体と14面体からなる充填である（1993年にこれが発見されるまでは切頂八面体がそうだった）。しかし、ある種の制約（例えば、孔が貫通していなければならない、問題となる空間が薄っぺらい、複雑な立体加工はできない、など）の下では、正六角柱が答えとなる。 自然界のハニカム構造 ハチの巣 昆虫の複眼 亀の甲羅 間質性肺炎の病変 玄武岩の柱状節理などに見られるように…
Wikipedia

通報 ...