x座標(奥行き) 3~6
y座標(高さ) 0~1
z座標(幅) 4~6
w座標(時間) 3~5
これらを満たす直方体を描いたんだが、こうなるのか。
人間が観測できるのは、時間が3~5であるときだけ。ということになるな。
…ただ、未来から過去に向かってボールを投げるとした場合、そのボールが とある現在 とただ一点においてのみ交差する…ということになるから、人間が観測できるのは一瞬であるよね(そもそも観測すらできない、限りなく0に近い交点になるんだろうけど)
ややこしいことに、時間という存在を、我々が生きている現在という時間と、自在に行き来できる時間とで分けて認識しなければならないから少し厄介だな。
いっそのこと時間を
過去、現在、未来という分け方ではなく。
ある瞬間より前、ある瞬間、ある瞬間より後。
という三要素によって時間が成り立っているとみなした方が上手くいくのでは。
マリオの話だけど、TIMEが進んでいる間左右から壁が迫っていて、0になった瞬間マリオが押しつぶされる…って解釈すると恐ろしい話だよな。
通報 ...
投稿するにはメンバーである必要があります。











w軸方向に移動する物体を特定した話は聞いたことがないので何とも言えないけど
その物体のw軸方向に対する幅と移動する速度次第じゃないか?
俺たちが(w=0)の3次元空間にいると仮定すると
俺たちが観測できるのは『4次元的な物体を(w=0)で分断したときの断面図のみ』ってことになる。
前回CTスキャンの例を少しだけ出したけど、「3次元構造物(人体)を2次元的に観測すると、その瞬間にスキャンしてる場所の2次元的な断面図になる」ってのと原理は同じ感じかと。
俺たちは3次元しか認識できない。
そして、上図で示されている、クセの強い部屋に住んでいる霧雨も同じく3次元の住人だ。
彼が点Pを見つめたとき視界に映る景色は「台形が2つと三角形が1つある平面」だ。
そう、3次元的存在であるはずの俺たちの視界は平面なんだ。
しかし、歩けば近づいたり遠ざかったりできることを俺たちは知っている。
なので平面でしかない視界が実際には3次元的なものだ(奥行きがある)と俺たちは認識することができている。
これを元にして、異なる次元について類推していこう。
まずは、2次元の世界に住んでいる霧雨がいたとする。
図で示したように、彼が見ている景色は恐らく1次元だろう。
彼の視界は幅のない線であるにもかかわらず、歩けば近づいたり遠ざかったりできることを彼は知っているので
線でしかない視界が実際には2次元的なものだ(奥行きがある)と彼は認識できているはずだ。
以上を踏まえると、4次元的存在の視界は3次元ではなかろうかと類推できるはずだ。
で、そこでややこしくなってくるのが『3次元的な断面図って何?』って話なんだけど
それが超立方体のような多胞体なのでは?と俺は解釈してる。
これ以上はもう俺の言語力が限界突破する(画力はとっくに限界を迎えてる)領域なので霧雨の想像力に頼りまくるしかないんだけど
4次元的存在である霧雨は、w,x,y,zの4軸方向に動ける。
そして、そんな彼の視界は恐らくx,y,z座標で表される3次元の景色であるはず。
さらに、彼が歩いたら視界にある3次元の光景も連動して超立方体のようにウネウネ動く。
俺のイメージはそんな感じ。
単純に感心するしかない。
なんとなく知ってるような話から知らなかった話まで分かりやすく説明くださりありがとうございます。
四次元について、俺からはこれ以上出せるカードがないので、いまだ唯一解消できていないこの疑問だけ解決させたいんだ。
空間の話に時間という異なる概念が割り込んで、あまつさえ一つの軸として居座りやがっていいものなのか?
物事を理解するための手段としてはアリだが、空間の話である以上は時間を軸として取り入れるのは正しくないんじゃないのか?
間違ってるかもしれんが自己解決できそう。いや、ビミョー。
一次元が直線、二次元が平面、三次元が空間…であるから、
四次元になった時点で空間ではない…ということか??
空間でない以上、w軸が時間であったところでなんの問題もないのか…??
腑には落ちないがそういうことなら理にかなってると言えなくもない。こじつけな気がしてならないが。
今まで「~ということになる」とかさんざん言い切ってきたけど、結局のところ俺もシロウトだからな。
イメージしやすさを優先して整合性とかは後回しにしてるし、くれぐれも俺が発信する文章を過度に信用しすぎないようにしてくれ。
ディスカバリーチャンネルを見る頻度が少しだけ多い、あくまでその程度です。
あ、ちなみに、晩飯食いながらよくこのシリーズを見てます。
4次元のそれを空間と呼ぶかどうかは権威ある学者に任せるとして、少なくとも性質は俺たちが見てる世界とぜんぜん違うだろうね。
>> 24でも使ったけど「類推」ってのは非常に便利でして。
2次元の住人も3次元の住人も、見えている景色に対して近づいたり遠ざかったりする・・・つまり「運動」を通してようやく自分のいる次元が何次元なのかを認識しているってわけだ。
部屋の隅にある点Pを見つめる霧雨の視界は、前回貼った図では「台形が2つ、三角形が1つ」だったけど、点Pから遠ざかればそのうち「台形が2つ、5角形が1つ」になるはずだ。
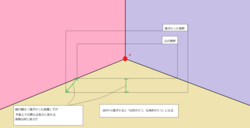
遠ざかった距離を示す緑の線の長さは実際には同じ距離であるはずなのに、「3次元を2次元に変換した図」では場所によって見かけ上の長さが異なることが確認できる。
超立方体における「この面が正方形なんて信じられねーんだが?」ってのも、同じ要領で起こってる現象じゃないだろうか?
しょうじき俺も意味分かってないんだけど、時間と空間を混ぜ合わせた「時空」って言葉はとりあえずあるよな。そんな感じの扱いでよくね?
ベクトルを持つものなら次元を構成する軸になり得ると思うよ。
「このままx軸上を真っすぐに進み続けたら、宇宙の外に出るんだろうか?その先はどうなってるんだろうか?空間に行き止まりはあるのか?」と3次元的な限界について考えることは可能だ。
それと同じで「時間の軸をこのまま進み続けていったら、いつか終点に辿り着くんだろうか?それとも無限に続くのだろうか?」と考えることも可能なはずだ。
拭いきれない微妙な違和感は残るかもしれないけど、一応は軸として機能しそうな気はする。
そういう意味では、温度のベクトルを色で表すサーモグラフィーなんかも4次元的だな。