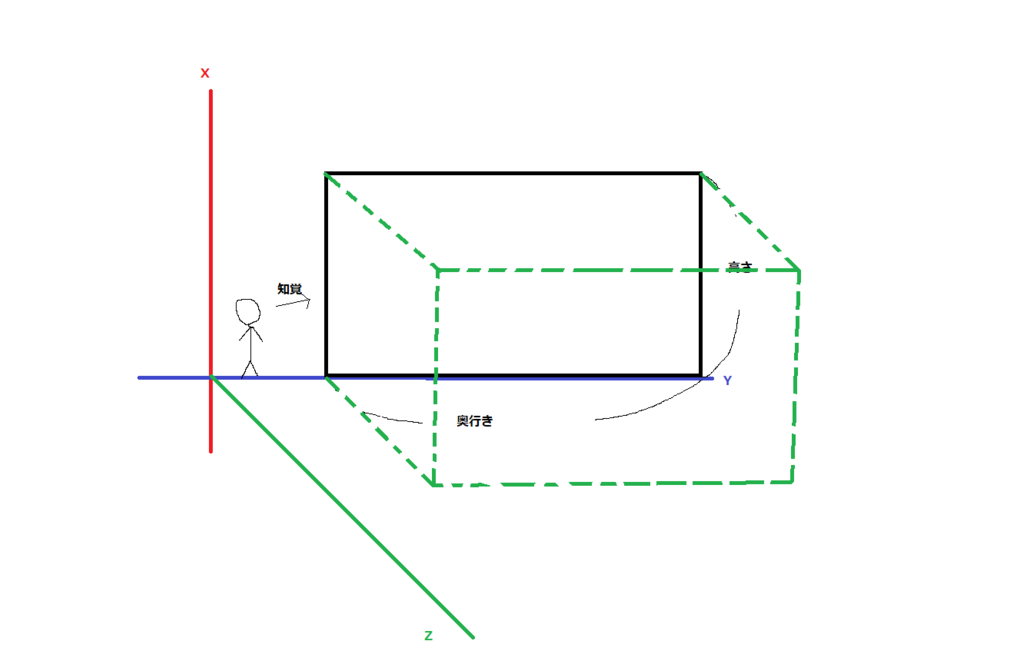
画像のクオリティについては敗北を認めるしかないわけだが
その自画像くんは「座標」の認識を少し誤解している。
0、1、2...と時間を加えることで直方体が特定の方向に連続しているわけだけど
つまりそれは

上図のように、Z軸を時間としていることになる。
この場合、軸は3本しか使われていないので第4の軸に時間を当てはめていることにはならない。
Z軸が時間であるなら、X軸とY軸はどうなるのか。
「縦/横/奥行」の要素をXとYに割り当てようとしても1つ余ることになるよな。
というわけで、とりあえず「横」を余らせてみよう。
つまり自画像くんが示している図はX軸が奥行きでY軸が高さ、Z軸は時間ということになる。
すると、この図と一致するはずだ。
横線をYにして縦線をXにしてるのマジでセンスないってことに今さら気付いたわけだが
それはさておき、つまるところ「高さと奥行きと時間」の軸で作られた3次元ということだ。
4次元以降を図示する(3次元に変換する)のが難しいってだけだよ。
同じ場所に5分のあいだ放置されていた立方体は
3次元的には静止している状態だけど、4次元的にはW軸方向に5分に相当するサイズを持っていることになるんだよ。正確な表現ではないけど。
そのことを示すために、もう1つ例を出そう。
スーパーマリオのような横スクロールゲームには「前後/上下」の2つの軸しかない。
なのでマリオが前方から進んでくるカメを避ける方法は「上を飛び越える」あるいは「下をくぐる」の2つしかない。マリオの世界には左右の軸がないので「横をすれ違う」という避け方はできない。
そのマリオに向かって横方向からボールを投げたとする。
その場合、マリオの視点では『何もないところから突然ボールが現れた』ように見えるわけだ。

もともと平面であるマリオの世界にはそもそも球体って概念もないんだが
マリオにとって視認可能なのは「Z座標が0のときだけ」なわけだ。
医療シーンで頭からつま先にかけてCTスキャンをかけたとき連続する断面図が映るだろ。そんな感じだ。
そのイメージを応用してくれ。
俺たちは3次元の世界しか捉えることはできない。
その俺たちに向かって4次元の方向からボールが投げられたら、俺たちは「w座標が0のときだけ」そのボールを視認することになる。
というわけで
空間・空間・空間ときていきなり時間が割り込んでくることにはどうしても違和感を覚える
これに関して言うなら
「未来から過去に向かって投げられたボール」があったとして、俺たちは時間の座標が俺たちと一致する瞬間だけそのボールを視認することが出来るというわけだ。
しかし、そのボールはw座標(過去←→未来)の方向に広がる全貌のうちの断面図にすぎないわけで、その全体図を想像するなら>> 13で言ったように4次元的な棒状になるのではないかな。