アカウントを作ったので試験的にトピックを立ててみます。
このトピックでは地頭を鍛えることを目的としています。
お互いにクイズを出題し合ってそれにチャレンジしてください。
「論理クイズ」とか「なぞなぞ」みたいな特別な知識を必要とせず発想力だけで解けるものが好ましいです。
回答するときや答えを載せるときなどヒント・ネタバレになりかねないときはそれを明記した上で
コンテンツ
を使ってください。
それからこのトピックでは暴言は禁止します。
ただし答えについて議論することもあると思うので、その過程で多少議論が白熱する程度なら許します。その代わり明らかな暴言やひねくれた態度などこのトピックの趣旨から大きく逸脱するのでやめてください。
このトピックはお互いを高め合う場であって、お互いを攻撃し合う場所ではありません。
あれ？
ログインしていたはずなのに....。
はい、なんかちょっとトラブっちゃいました。すいません。
まだあんまりシステム理解できてないんです。すいません。
気を取り直して記念すべき１問目。
ネットから拾ってきたものだから見たことある人いるかもしれないけど、個人的に面白い問題だと思ったので選びました。
灰色の部分の面積が９になるとき、長方形ABCDの面積を求めてください。
解答はまた後で載せます。
面白い問題っていうかおかしい問題だね
イラストからは
x-4＞y
x=2y-6
が導き出せる。
上の式のxに2y-6を代入して整理すると
y＞10が得られる。
で、灰色の部分の面積をyを使った方程式で表すと、
y×(y-8)=9
これを解くと、
y=-1、9
y＞10と矛盾してる。
おかしいよな？
俺のやり方がおかしいのか問題がおかしいのか、答えに期待。
もちろん、最初はバカ正直に計算して
この問題の答えは96だって言おうと思ったよ。
けど、それだと右上の長方形の面積が99になるからおかしいことに気付いたんだよ…。
問題の前提がおかしいってことで、いいよな？
どうせ、もっと厳密におかしい理屈を説明しないと正解にならないんだろうけど…
「惜しい！」とか言って「実はこういうカラクリなのだ！」とか嬉嬉として説明してくるナチュラルのドヤ顔を思い浮かべると
死ぬほど不快すごく素敵なので寝るわおやすみ※追記
ラベルつけました。
これ無理くね？
Yは10より大きくなければいけないけど、それだと面積9が求まらない。
お手上げです。
面白い…のか…？この問題の面白さが理解できん。
これ問題おかしいだろ。出題者がおかしいから当然か。きっと自分で解けないから誰かに解いてもらおうとしたんだな。はーあ。
いや、たぶんそういう事ではないと思うぞ。出題者は「問題がおかしい」というのが答えだっていうのが面白いってことだと思う
これみたいな感じ
まあ、長方形の問題については灰色のやつが長方形とは限らないから、問題がおかしいというかそれ以前に前提がガバガバだけど
灰色部分の面積は
20より大きくないとだめなはず
答え早く 眠れない
x-8を＠にすると各辺の長さは次の通り。＠は２超でないとならないけどそうすると９になりようがない。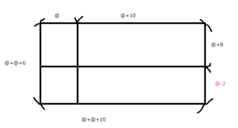
さっき書いたけど、期待される問題の答えは「問題がおかしい」だよ。「そんな問題あるか！」って思う人は上のコメントのリンク見てね。この長方形の問題は知らなかったけどこういう系統のやつは割と有名。
なんかわからんけどすごくむなしくなった、、、
思ったより伸びてた。
というわけで以下>> 1の解答です。
正解は「解なし」です。皆さんの仰る通り灰色の部分の面積が９のとき長方形ABCDは成り立ちません。
この問題の何が面白いかって？
人によってリアクションが違うところだよ。
この問題はネット上に投稿された問題で、SNS等では色んなリアクションが垣間見れて非常に面白かったです。
けっこう性格現れちゃうよね。
続いて第二問。
Ａ，Ｂ，Ｃ，Ｄ，Ｅの箱にそれぞれ８，２１，２６，２，１８個のボールが入っています。
これから皆さんには入っているボールの個数を全て均等にしてもらいます。
この５つの箱はＡＢＣＤＥ円形に並んでいて、１つのボールは隣同士にしか移動させることはできません。
１つのボールを移動させるごとに１回とカウントするとき、最低何回あれば均等にできるでしょう？
考え方も含めて回答してみてください。
単に平均値である15になるように、それぞれ1個ずつ移動するだけっていうクソ問じゃないよな？
答え20だったら、第一問目に続きクソ問続きなので、マジでクソだわ。
えっと、皆さん答えるときはちゃんと
コンテンツ
使ってくださいね。
それと>> 18さん、なぜそれが最低回数になるのか考え方（証明）とかないのならちょっと残念です。
そりゃ１個ずつ移動してればいつか均等にはできますけど、あくまでもこの問題は最小手を問う問題です。
Aが8 Dが2 これらの箱を15にするためには、
B6個E1個をAに移動
C11個E2個をDに移動
普通の答えが、無駄のない最善の動きのように見えますので答えは20となります。
それとも、これで4回とカウントするのですか？
今のところ、俺が考えうる中での最小は11回です。以下、考え方を説明。
🔶問題が10進数で書かれている場合
※箱には合計75個のボールが入っているため、15個×5に分けるか25個×3に分けるかを考える必要がある。
🔸全ての箱に均等に入ってる必要がある場合 20回
8 21 26 2 18
14 15 26 2 18 （6）
15 15 26 2 17 （7）
15 15 15 13 17 （18）
15 15 15 15 15 （20）
🔸ボールの入ってない箱があってもいい場合 11回
8 21 26 2 18
8 22 25 2 18 （1）
5 25 25 2 18 （4）
0 25 25 2 23 （9）
0 25 25 0 25 （11）
🔶問題が9進数で書かれている場合
※10進数に直すと合計が70になるため、必然的に14個×5に分ける必要がある
🔸全ての箱に均等に入ってる必要がある場合 18回
8 21 26 2 18
8 19 24 2 17 （10進数に変換）
13 14 24 2 17 （5）
14 14 24 2 16 （6）
14 14 24 4 14 （8）
14 14 14 14 14 （18）
🔶問題が11進数以上で書かれている場合
※10進数で書かれている場合のときと比べると、10進数に直した時にボールの数が増えてしまうだけなので考えないものとする。
〇進数、という考え方は「特別な知識」に含まれますか？